🔍 문제보기
문제:
하나의 집합을 의미하는 문자열을 입력받아 각 문자를 가지고 만들 수 있는 모든 부분집합을 리턴해야 합니다.
입력:
| 인자1 : N |
|
출력:
- 배열(arr)을 리턴해야 합니다.
- arr[i]는 각 부분집합의 원소로 구성된 문자열
주의사항:
- arr[i]는 각 부분집합을 구성하는 원소를 연결한 문자열입니다.
- arr[i]는 알파벳 순서로 정렬되어야 합니다.
- 집합은 중복된 원소를 허용하지 않습니다.
- 부분집합은 빈 문자열을 포함합니다.
- arr은 사전식 순서(lexical order)로 정렬되어야 합니다.
입출력 예시:
let output1 = powerSet('abc');
console.log(output1); // ['', 'a', 'ab', 'abc', 'ac', 'b', 'bc', 'c']
let output2 = powerSet('jjump');
console.log(output2); // ['', 'j', 'jm', 'jmp', 'jmpu', 'jmu', 'jp', 'jpu', 'ju', 'm', 'mp', 'mpu', 'mu', 'p', 'pu', 'u']
📝 이 문제는...
이 문제는 쉬울줄 알았는데, 머리속에 떠오르는 대로 코드를 짜다보니 함정들이 불쑥불쑥 튀어나와서 의외로 고전했던 문제였다.
역시 방심하지 말고 먼저 세부적으로 그려보고 규칙을 뽑아내는 과정은 필수 인 것같다.
결과적으론 가능한 조합을 하나씩 그래프로 그려보면 풀 수 있었다.
💡추가 상식
이문제의 이름 powerset은 한국어로 '멱집합'을 말한다. 집합론에서 멱집합은 주어진 집합의 모든 부분 집합들로 구성된 집합을 말한다.

💡 잠깐! 아이디어 생각해보기
일단 나에게 엄청난 알고리즘 지식은 없지만, 그것을 대체할 수 있는 가능성이 있다.
그건 바로 '단순화' 와 '노가다'!!
바로 단순화시켜서 일일이 그려보자.
만약 단순하게
powerSet('abcd');라는 문자열이 함수에 들어왔을 경우 어떤 배열이 나와야 할까?
아래의 그림으로 그려보았다.
(물론, 이 경우는 알파벳이 착하게도 순서대로, 중복없이 들어왔지만, 이런 엣지케이스 핸들링은 문제의 핵심은 아니므로,
일단 그냥 착한 경우로 문제의 핵심을 파악해본다.)
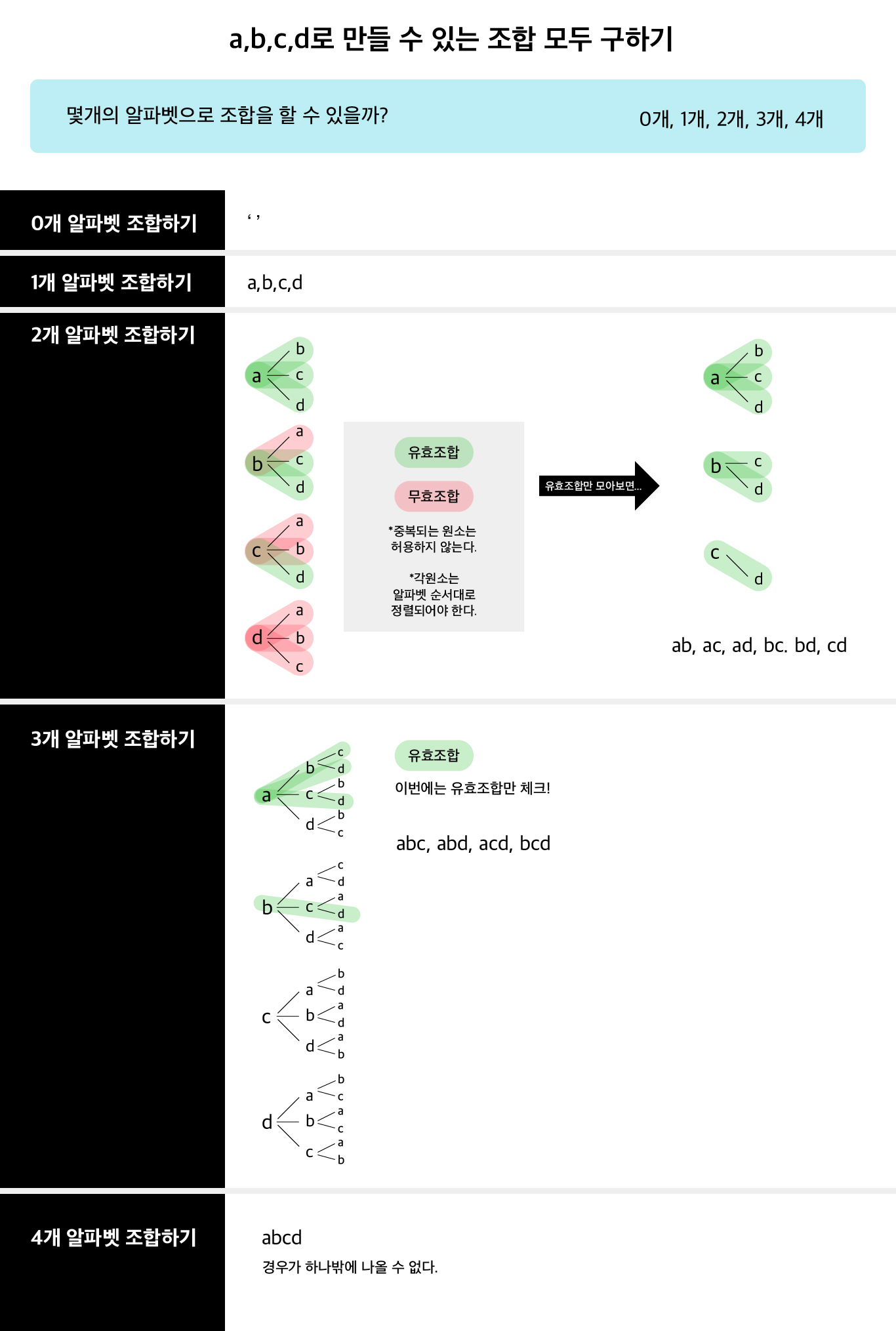
이 나온 조합들을 알파벳 순서대로 정리하면 아래와 같이 나올것이다.
['', 'a', 'ab', 'abc', 'abcd', 'abd', 'ac', 'acd', 'ad', 'b', 'bc', 'bcd', 'bd', 'c', 'cd', 'd']
이 배열은 원소의 조합이 중복되지 않고, (abc,acb ❌) 모두 알파벳순으로 정렬되어 있다. (abc ⭕️ acb❌)
근데 여기까지 무식하게 적어보면 뭔가 규칙이 보인다.
아래의 2,3,4개 알파벳 조립하기 경우를 보자.
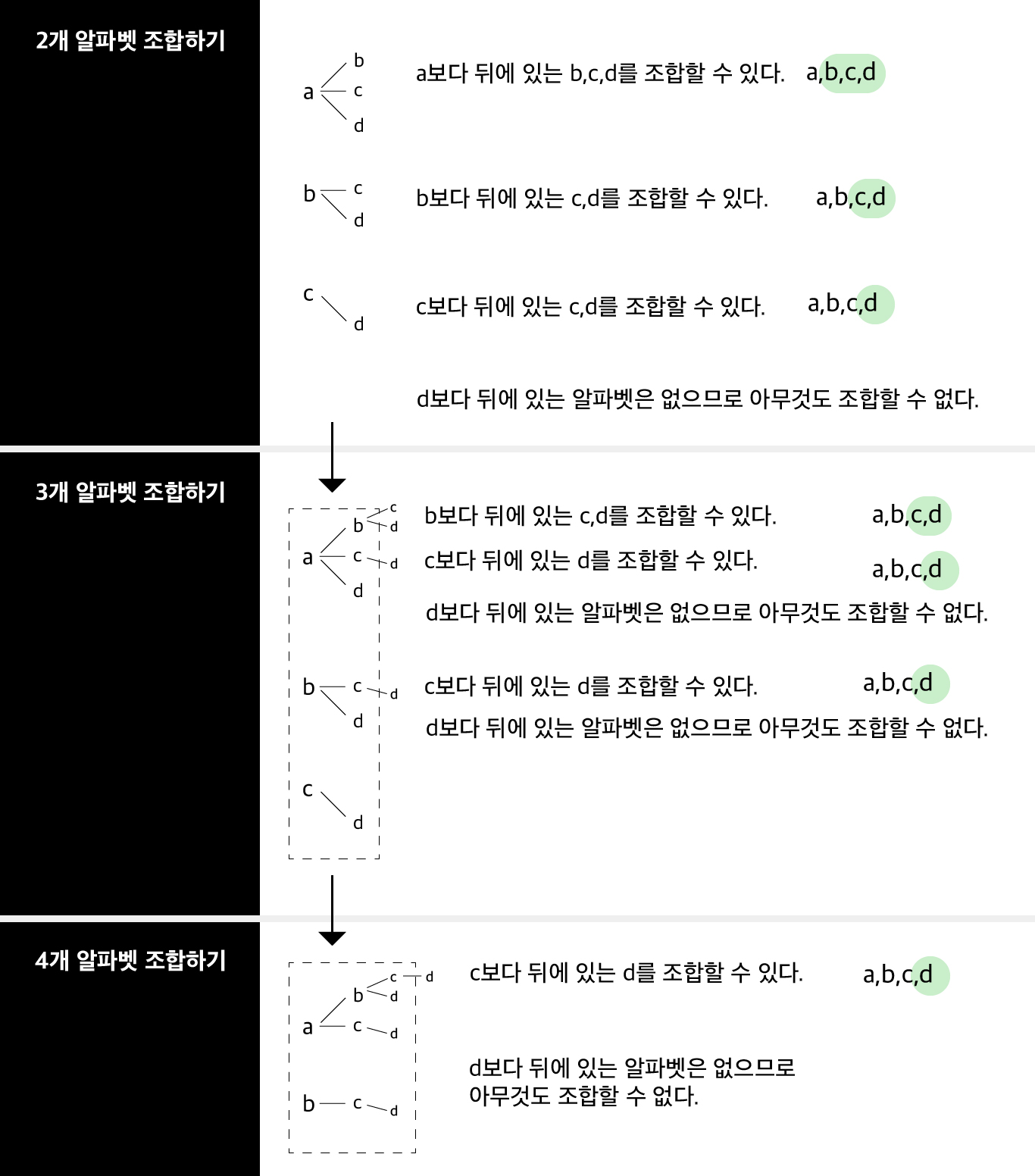
다음의 규칙을 추릴 수 있다.
1. 이전 갯수조합에서 구했던 원소들에서 가지를 뻗어나간다.
2. 가지를 뻗어나갈 때는 당연히 마지막 원소(ex.b)보다 뒷 순서(ex.c와d)의 알파벳이 있을 경우만 뻗어나간다.
나는 개인적으로 이렇게 아주 단순한 노가다로 규칙을 발견했다.
이제 이것을 전처리, 후처리와 함께 코드로 적어보았다.
🌟 문제풀이
const powerSet = function (str) {
const base = [...new Set(str)].sort() //중복제거하고 오름차순으로 놓기 'dddcaab' -> [a,b,c,d]
//base는 계속해서 알파벳 순서를 파악하는 데에 쓰인다.
let result = ['',...base] //원소길이 0일때, 1일때 미리 넣어놓기 ['',a,b,c,d]
let charNum = 2; //조합할 원소의 길이 (0일때와 1일때는 미리 그냥 넣어버렸으니, 2부터 시작)
let startIdx = 1; //이전갯수 조합 턴에 추가를 시작한 idx (기본은 원소길이 0인 경우 제외한 시작점)
let endIdx = base.length; //이전갯수 조합 턴에 추가를 끝낸 idx
while(charNum <= str.length){ //뽑고자 하는 원소의 길이가 base의 길이보다 적다면 반복(같아진다면 stop됨)
const newElemArr = [] //이번 턴에 추가할 원소들의 배열()
for(let i=startIdx; i<endIdx; i++){
let prevElem = result[i]
let prevElemLastChar = prevElem[prevElem.length - 1]
let prevElemLastCharIdx = base.indexOf(prevElemLastChar)
//위 세줄은 아래의 한줄로도 요약 가능
//let prevElemLastCharIdx = base.indexOf(result[i][result[i].length - 1])
if(prevElemLastCharIdx < base.length - 1){ //만약 조합할 수 있는 알파벳이 있다면(a,b,c,d중 d로 끝난게 아니라면)
for(let j=prevElemLastCharIdx + 1; j<base.length; j++){
newElemArr.push(result[i] + base[j])
}
}
}
result = [...result,...newElemArr] //0개,1개 조합 result에 새로운 2개조합을 더해준다.
startIdx = endIdx + 1 //ex. 두개조합의 시작점 (이제 세개 조합할때 구해놓은 두개조합 이용)
endIdx = endIdx + newElemArr.length //ex.두개조합의 끝지점 (이제 세개 조합할때 구해놓은 두개조합 이용)
charNum++ //ex. 두개알파벳 조합 찾았음 이제 세개로 넘어가야함
}
return result.sort()
};
🌟 문제풀이2 : 재귀이용 참고 코드
정답 코드는 재귀를 사용해서 풀었는데, 확실히 재귀가 이해하긴 어렵지만 결과적으로 보았을땐 더 단순해 보이긴 한다.
재귀 방식은 추후에 기회가 된다면 또다른 해설로 풀어 적어봐야겠다.
const powerSet = function (str) {
// 정렬
const sorted = str.split('').sort();
// 중복 제거
const deduplicated = sorted.reduce((acc, item) => {
if (acc[acc.length - 1] === item) {
return acc;
} else {
return acc.concat(item);
}
});
let subSets = [];
const pickOrNot = (idx, subset) => {
// base case
if (idx === deduplicated.length) {
// 마지막 문자까지 검토한 경우
subSets.push(subset);
return;
}
// recursive case
// idx번째 문자가 포함되지 않는 경우
pickOrNot(idx + 1, subset);
// idx번째 문자가 포함되는 경우
pickOrNot(idx + 1, subset + deduplicated[idx]);
};
pickOrNot(0, '');
return subSets.sort();
};

'알고리즘' 카테고리의 다른 글
| Greedy Algorithm 탐욕 알고리즘 기본 + 예제 (0) | 2022.10.18 |
|---|---|
| getItemFromTwoSortedArrays 문제 뜯어보기 (0) | 2022.10.04 |
| orderOfPresentation 문제 뜯어보기 (0) | 2022.09.27 |
| rotatedArraySearch 문제 뜯어보기 (0) | 2022.09.18 |
| treeBFS 문제 뜯어보기 (0) | 2022.09.16 |



