😋 탐욕 알고리즘이란?
이름부터 greedy, 탐욕 말그대로 "탐욕스럽게" 그때그때 좋은걸 선택해서 조건에 부응하는 가장 최적의 조합의 값을 찾는 계산법이다.

사전적 정의는 아래와 같다.
탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
다소 어려운 정의를 풀어서 설명하자면,
"최적해를 구하는 데에 사용되는"
여기서 '최적해'를 구할때 탐욕알고리즘이 사용된다고 했는데
여러개 중에 골라서 최대 혹은 최소의 값을 만들어야 할때,
(다시말해, 몇가지를 선택하여 최적의 값을 만들어야 할때) 그 최적 값을 구하는 데에 사용된다는 것이며
"근사적 방법"
'근사적'이라는 말을, 모든 경우에 정확한 최적해는 아니지만,
직관적으로 가까운 답에 빠르게 이르는 알고리즘이라는 사실을 알 수 있다.
📌 탐욕 알고리즘의 문제 해결 단계
탐욕 알고리즘을 사용해서 최적해를 구할때 문제를 해결해나가는 단계들이 정해져있다.
- 선택 절차(Selection Procedure) : 현재 상태에서 최적의 해답을 선택한다.
- 적절성 검사(Feasibility Check) : 선택된 해가 문제의 조건을 만족하는지 검사한다.
- 해답 검사(Solution Check) : 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.
😶🌫️ 탐욕 알고리즘 기초 예시
탐욕 알고리즘의 가장 기초적인 예시 두가지를 보자면 아래의 두가지가 있다.
- 동전갯수 가장 적게 거스름돈 돌려주기
- 용량이 제한되어 있는 가방에 가장 값비싼 물건으로 채우기
이 두가지 경우를 탐욕알고리즘의 관점에서 생각해보자.
📌 동전갯수 가장 적게 거스름돈 돌려주기
맛있는 걸 사먹기 위해 편의점 알바를 하는 커비. 와들디가 손님으로 찾아와서 4,050원어치 물건을 샀다.
와들디는 계산을 하기 위해서 5,000원을 내밀며, 동전이 짤랑거리는게 싫으니 최대한 동전을 적게 달라고 말했다.
이때 커비는 500원, 100원, 50원, 10원 동전을 어떻게 조합해서 줘야 할까?

탐욕 알고리즘 적용 절차에 따라서 문제를 해결해보자!
사실 우리는 항상 거스름돈을 줄때 탐욕알고리즘을 이용하고 있고 당연하지만,
컴퓨터한테 알려준다 생각하고 하나하나 풀어적어본다.
- 선택 절차 : 500원짜리로 최대한 많이 줘야 동전이 줄겠지? 500원짜리 2개 먼저 거슬러 주자! (500원*2)
- 적절성 검사 : 엥? 500*2는 1,000원, 거스름돈은 (5,000 - 4,050) 950원 이어야 하는데? 적절하지 않네! 다시 1번으로
- 선택절차 : 500원짜리 하나빼고 그 다음으로 비싼 100원짜리 동전을 넣어보자. (500원*1, 100원*5)
- 적절성 검사 : 엥? (500*1) + (100*5) 1,000원은 950원을 넘잖아? 다시 1번으로!!
- 선택절차 : 100원짜리 하나 빼고 그 다음으로 비싼 50원짜리 동전을 넣어보자 (500원*1, 100원*4, 50원*1)
- 적절성 검사 : (500*1) + (100*4) + (50*1) 은 950원을 초과 하지 않는군, 적절해!
- 해답검사 : (500*1) + (100*4) + (50*1) = (5,000 - 4,050) 거스름돈과 동전 조합의 값이 동일!
- 정답 : 500원 1개 / 100원 4개 / 50원 1개
이렇게 그때그때 가장 값어치가 높아서 '동전의 갯수가 가장 적게 거스름돈에 도달하는' 최적해를 구하는 데에
가장 적합한 동전 순으로 성질 급하게 골라가면서
"아냐? 아님말고 그럼 그 다음 좋은거 넣지뭐!" 라는 식으로 진행되는
다소 터프한 알고리즘이다.
📌 용량이 제한되어 있는 가방에 가장 값비싼 물건으로 채우기
커비가 지게 음식을 담으려 한다. 커비의 지게는 35kg를 넘으면 부서져버린다.
커비가 담고 싶은 음식들은 모두 무게가 다른데, 4종류가 정해진 양만큼 있다.
이왕 이렇게 된거 양보다 질이라고, 커비는 가격에 비해 무게가 적게 나가는 음식으로만 지게를 채우고 싶다고 한다.
커비는 지게를 어떻게 채워야 할까? (단, 음식은 g당으로 쪼개어 넣을 수도 있다.)
🥦 : 총 3달러 40kg / 1달러당 13.3kg
🍠 : 총 1.5달러 25kg / 1달러당 16.7kg
🎂 : 총 2.5달러 5kg / 1달러당 2kg
🍉 : 총 2달러 20kg / 1달러당 10kg

이번에는 다시 돌아가는 적절성 검사 , 해답 검사는 생략하고 잘 선택한 경우만 뽑아서 절차 없이 쭉쭉 선택해보자!
- 선택 절차 : 1달러당 2kg으로, 무게대비 가장 비싼 🎂 먼저 최대 5kg으로 담는다. (남은 지게 무게: 35 - 5 = 30kg)
- 선택 절차 : 그 다음 가장 무게대비 비싼 🍉 를 최대 20kg으로 담는다. (남은 지게 무게: 30 - 20 = 10kg)
- 선택 절차 : 그 다음 가장 무게대비 비싼 🥦를 최대 10kg 어치만 담는다. (남은 지게 무게: 10 - 10 = 0kg)
- 정답: $2.5 + $2 + $0.75(3/4) ⇒ 커비는 최대 $5.25어치의 음식을 담아갈 수 있다.
위 두가지 예시로 탐욕 알고리즘이 엄청 쉽고 좋아보이지만, 꼭 그렇지만도 않은 순간이 있는게
커비가 음식을 "몇원어치"만 담을 수 없는 상황이었을 수 있다.
그런 상황일 경우 탐욕 알고리즘은 5kg의 빈자리를 10kg을 채우지못했을텐데,
사실 탐욕 알고리즘을 따르지 않으면 더 나은 조합이 있을수도 있기 때문이다.
그래서 탐욕 알고리즘은 제한적인 상황에서만 이용할 수 있다.
🫡 탐욕 알고리즘 적용 조건
- 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
- 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
커비가 음식을 골랐다고 이후 다른 빵을 고르는데 또다른 조건이 없어야하고,
커비가 음식을 전체가 아니라 덜어가서라도 최적의 해결방법을 냈을 때, 그것은 최종 문제 해결 방법이된다.
(만약 커비가 음식을 통째로만! 가져가야 한다면 부분 문제에 대한 최적문제 해결방법이 최종 해결방법이 아닐 수도 있을것이다.)
추가로 아래의 그림처럼 트리 구조에서 탐욕 알고리즘은 매우 부정확한 결과를 가져올 수 있다.
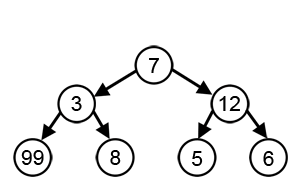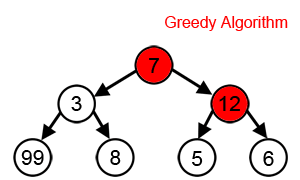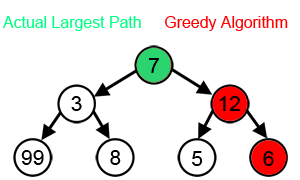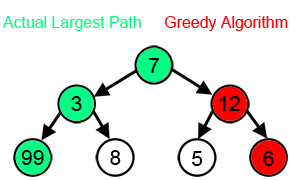
이제 본격적인 문제로 탐욕 알고리즘을 만나보자!!
📦 문제01 : 짐나르기
문제:
김코딩과 박해커는 사무실 이사를 위해 짐을 미리 싸 둔 뒤, 짐을 넣을 박스를 사왔다. 박스를 사오고 보니 각 이사짐의 무게는 들쭉날쭉한 반면, 박스는 너무 작아서 한번에 최대 2개의 짐 밖에 넣을 수 없었고 무게 제한도 있었다.
예를 들어, 짐의 무게가 [70kg, 50kg, 80kg, 50kg]이고 박스의 무게 제한이 100kg이라면 2번째 짐과 4번째 짐은 같이 넣을 수 있지만 1번째 짐과 3번째 짐의 무게의 합은 150kg이므로 박스의 무게 제한을 초과하여 같이 넣을 수 없다.
박스를 최대한 적게 사용하여 모든 짐을 옮기려고 합니다.
짐의 무게를 담은 배열 stuff와 박스의 무게 제한 limit가 매개변수로 주어질 때, 모든 짐을 옮기기 위해 필요한 박스 개수의 최소값을 return 하도록 movingStuff 함수를 작성하세요.
입력:
| 인자1 : stuff | 인자1 : limited |
|
|
출력:
- Number 타입을 리턴해야 합니다.
- 모든 짐을 옮기기 위해 필요한 박스 개수의 최솟값을 숫자로 반환합니다.
주의사항:
- 옮겨야 할 짐의 개수는 1개 이상 50,000개 이하입니다.
- 박스의 무게 제한은 항상 짐의 무게 중 최대값보다 크게 주어지므로 짐을 나르지 못하는 경우는 없습니다.
입출력 예시:
let output = movingStuff([70, 50, 80, 50], 100);
console.log(output); // 3
let output = movingStuff([60, 80, 120, 90, 130], 140);
console.log(output); // 4
정답:
function movingStuff(stuff, limit) {
//stuff = 짐의 무게를 담은 배열
//limit = 박스의 무게 제한
//return 모든 짐을 옮기기 위해 필요한 박스 개수의 최소값
//조건 = 한번에 두개, 무게 제한
stuff.sort((a,b) => a-b) //[50,50,70,80]
let boxCount = 0;
while(stuff.length !== 0){ //짐이 아직 남았다면
if(stuff[stuff.length - 1] + stuff[0] > limit){ //📌
//limit 초과 했다면 가장큰거 하나만 넣어야함
stuff = stuff.slice(0,stuff.length - 1); //가장 큰거 짐 목록에서 빼기
}else{
//가장 큰 거 + 가장 작은 <= 무게제한
stuff = stuff.slice(1,stuff.length - 1); //가장 작은거 가장 큰거 짐 목록에서 빼기
}
boxCount++
}
return boxCount
}
//📌에서 stuff[stuff.length - 1] + stuff[0]으로 선택 기준을 잡은 이유
//가장 큰 거 + 가장 작은 거 > 무게제한
//(가장큰거는 가장작은거랑 안들어갔음 무조건 혼자 들어가야함 => 명확)
//(작은것 끼리 빼면 나중에 큰거랑 조합해서 뺼 수 있음에도 박스 낭비 발생)
// 따라서 직관적으로 가장 큰거 + 가장 작은 거 부터 시작하는 조합이 가장 효율적일 것이라 판단
🤑 문제02: 편의점 알바
문제:
편의점에서 아르바이트를 하고 있는 중에, 하필이면 피크 시간대에 손님에게 거스름돈으로 줄 동전이 부족하다는 것을 알게 되었습니다. 현재 가지고 있는 동전은 1원, 5원, 10원, 50원, 100원, 500원으로 오름차순으로 정렬되어 있고, 각 동전들은 서로 배수 관계에 있습니다. 동전 개수를 최소화하여 거스름돈 K를 만들어야 합니다. 이때, 필요한 동전 개수의 최솟값을 구하는 함수를 작성해 주세요.
입력:
| 인자 : k |
|
출력:
- number 타입의 거스름돈 K원을 만드는데 필요한 동전 개수의 최솟값을 반환해야 합니다.
입출력 예시:
// 4000원을 받았을 때 500원짜리 동전 8개를 반환합니다.
const output1 = partTimeJob(4000);
console.log(output1); // --> 8
// 4972원을 받았을 때 500원짜리 동전 9개, 100원짜리 동전 4개, 50원짜리 동전 1개, 10원짜리 동전 2개, 1원짜리 동전 2개, 총 18개를 반환합니다.
const output2 = partTimeJob(4972);
console.log(output2); // --> 18
정답:
function partTimeJob(k) {
let count = 0;
const typeOfCoins = [500, 100, 50, 10, 5, 1];
for(let i=0; i<typeOfCoins.length; i++){
if(k === 0) break;
count += Math.floor(k/typeOfCoins[i]);
k %= typeOfCoins[i];
}
return count
}
이 문제에서 하나 짚고 넘어가야 할 것이 있는데,
🛑 greedy 알고리즘으로 문제를 풀기 위해서는 항상 동전들이 서로 배수관계에 있어야 한다는 점이다.
다른 말론 비슷한 문제에 '동전들이 서로 배수관계에 있다'라는 조건이 없다면
다른 알고리즘을 고려해봐야 한다는 말이다.
실제로 이렇게 그리디 문제는 제한적인 상황에서만 가능하다보니, 웬만하면 비슷한 유형에서
비슷한 수준으로 나오는 경우가 많다고 하는데,
만일의 경우를 대비해 시간이 될 때 탐욕 알고리즘 문제는 더 풀어보는 것도 좋을 것 같다.
'알고리즘' 카테고리의 다른 글
| getItemFromTwoSortedArrays 문제 뜯어보기 (0) | 2022.10.04 |
|---|---|
| powerSet 문제 뜯어보기 (0) | 2022.10.04 |
| orderOfPresentation 문제 뜯어보기 (0) | 2022.09.27 |
| rotatedArraySearch 문제 뜯어보기 (0) | 2022.09.18 |
| treeBFS 문제 뜯어보기 (0) | 2022.09.16 |



