getItemFromTwoSortedArrays 문제 뜯어보기
🔍 문제보기
문제:
길이가 m, n이고 오름차순으로 정렬되어 있는 자연수 배열들을 입력받아 전체 요소 중 k번째 요소를 리턴해야 합니다.
입력:
| 인자1 : arr1 | 인자2 : arr2 | 인자3 : k |
|
|
|
출력:
- number 타입을 리턴해야 합니다.
주의사항:
- 두 배열의 길이의 합은 1,000,000 이하입니다.
- 어떤 배열 arr의 k번째 요소는 arr[k-1]을 의미합니다.
입출력 예시:
let arr1 = [1, 4, 8, 10];
let arr2 = [2, 3, 5, 9];
let result = getItemFromTwoSortedArrays(arr1, arr2, 6);
console.log(result); // --> 8
arr1 = [1, 1, 2, 10];
arr2 = [3, 3];
result = getItemFromTwoSortedArrays(arr1, arr2, 4);
console.log(result); // --> 3
Advanced:
- 단순히 처음부터 끝까지 찾아보는 방법(O(K)) 대신 다른 방법(O(logK))을 탐구해 보세요.
힌트:
- 이진 탐색(binary search)을 응용하여 해결합니다.
📝 이 문제는...
극악의 난이도로 문제를 풀어보기는 커녕, 레퍼런스 코드 해석도 어려웠다. ㅜ
일단 시각화해서 생각해야 간신히 이해할 수 있었다.
🌟 정답
이번엔 풀기는 커녕 정답코드 이해하기도 힘들었으므로,,,
그냥 일단 정답코드부터 뿌리고 보겠다.
이 코드는 정답코드에서 내가 시각화하면서 이해하기 편하도록 변수명을 좀 바꾸고 주석을 추가한 코드이다.
이 코드를 보면서 아래의 이미지 해설을 본다.
// O(logK) solution
const getItemFromTwoSortedArrays = function (arr1, arr2, k) {
let topFirstValid = 0,
bottomFirstValid = 0;
while (k > 0) {
// 이진 탐색을 위해 각 배열에서 k를 절반으로 쪼개서 카운트 한다.
let half = Math.ceil(k / 2);
let topPortion = half,
bottomPortion = half;
// 엣지 케이스1(없어도 통과되나 불필요한 연산 없애기 위해 없어도 통과는 됨, but 더 오래걸림)
// 카운트가 남았음에도 배열의 끝에 도달하면 k를 나머지 배열쪽으로 넘긴다.
if (topFirstValid === arr1.length) {
bottomFirstValid = bottomFirstValid + k;
break;
}
if (bottomFirstValid === arr2.length) {
topFirstValid = topFirstValid + k;
break;
}
// 엣지 케이스2
// 현재 카운트가 남아있는 후보 요소들보다 많을 경우, topPortion(현재 할당량)을 남아있는 요소들의 개수로 바꾼다.
if (half > arr1.length - topFirstValid) topPortion = arr1.length - topFirstValid;
if (half > arr2.length - bottomFirstValid) bottomPortion = arr2.length - bottomFirstValid;
// 두 배열의 현재 검사 요소 위치를 비교해서, 그 값이 작은 배열은 비교한 위치 앞에 있는 요소들을 모두 후보군에서 제외시킨다.
if (arr1[topFirstValid + topPortion - 1] < arr2[bottomFirstValid + bottomPortion - 1]) {
topFirstValid = topFirstValid + topPortion;
// 처리가 끝나면 k값을 절반으로 떨어뜨린다.
k = k - topPortion;
} else {
bottomFirstValid = bottomFirstValid + bottomPortion;
k = k - bottomPortion;
}
}
return Math.max(arr1[topFirstValid - 1], arr2[bottomFirstValid - 1])
};
일단 위 코드를 보고 아래의 해설을 차례차례 보면서 이해해보자!!
🌟 해설
일단 이 문제는 보통의 이진탐색(binary search)처럼
몇개를 체크할 것인가,
어디서부터 체크할 것인가
이 두개의 사항을 좁혀나가면서 효율적인 탐색을 한다.
근데 보통의 이진탐색은 탐색범위가 하나이고, 그걸 반씩 갈라서 진행되는데 (일반적인 이진탐색 문제는 링크를 참고)
이건 이미 배열은 둘로 나뉘어 있고, 따로 들어온 k라는 숫자를 반으로 나눈다!!
K번째 큰 숫자를 구하기 위해
K를 반으로 나누어 두 배열에서 판별을 하는 과정을 거치는데,
아래의 그림이 그 과정을 대~강 보여준다.
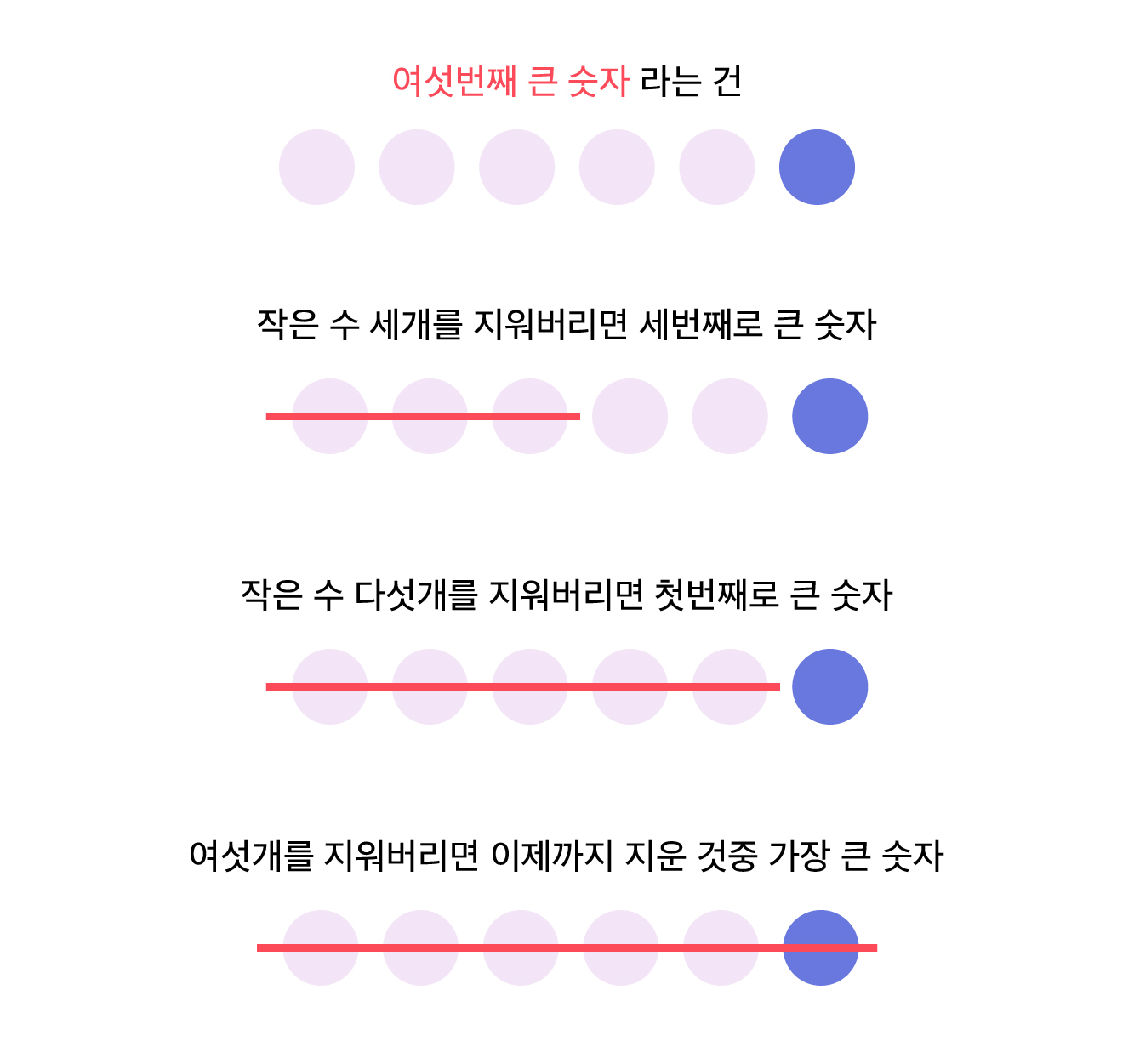

위와 같은 로직으로 이제 세부적으로 탐색 로직을 따라가보자!!
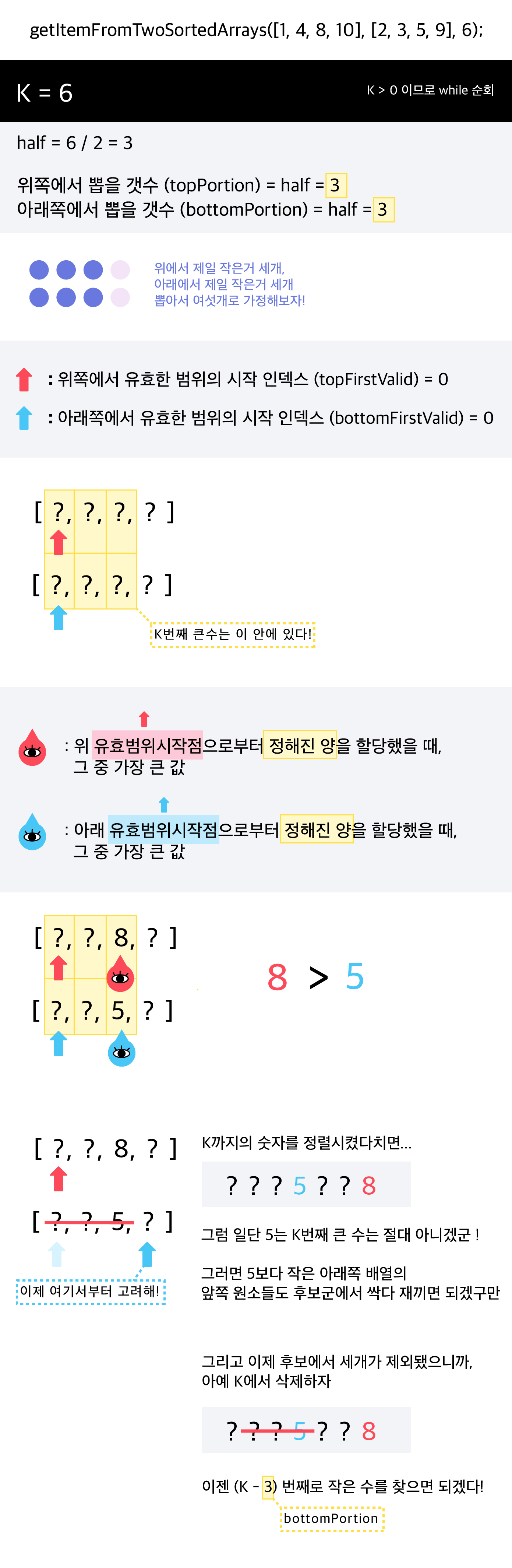


엣지 케이스 대응을 위해 예시 한가지를 더본다.

여기까지 해설 이미지를 보고 코드를 보면 좀 더 이해가 되...었으면 좋겠다.
이 문제는 레퍼런스 코드도 인터넷에 친절하게 해설되어 있는게 하나도 없고
그 자체도 이해가 어려워서,
이틀에 걸쳐서 여러 자료를 찾아보고 실험해보고 그림을 그려가면서 자료로 만들었다.
레퍼런스 코드를 조금더 (적어도 나는) 이해하기 쉽게 변수명들을 바꾸고
시각화를 시키고 나니 그나마 좀 이해가 가는 문제였다.
혹시라도 나같이 이 문제가 도무지 뭐가 뭔지 모르겠는 분들은 위의 자료를 보면서
조금 감을 잡으시길 바란다.
물론... 최선의 해설은 아닐 수 있다!
더 좋은 해설이 생각날만큼 알고리즘 고수가 되면 또 한번 복습하고 싶은 문제이다.
