알고리즘

treeBFS 문제 뜯어보기

칠뎁 2022. 9. 16. 01:25

🔍 문제보기

 

문제:

임의의 tree를 구성하는 노드 중 하나의 Node 객체를 입력받아, 해당 노드를 시작으로 너비 우선 탐색(BFS, Breadth First Search)을 합니다. 이 때, 탐색되는 순서대로 노드의 값이 저장된 배열을 리턴해야 합니다.

 

 

입력:

인자1 : node
  • 'value', 'children' 속성을 갖는 객체 (Node)
  • 'node.value'는 number 타입
  • 'node.children'은 Node를 요소로 갖는 배열

 

출력:

  • 배열을 리턴해야 합니다.

 

주의사항:

  • 생성자 함수(Node)와 메소드(addChild)는 변경하지 않아야 합니다.

 

입출력 예시:

let root = new Node(1);
let rootChild1 = root.addChild(new Node(2));
let rootChild2 = root.addChild(new Node(3));
let leaf1 = rootChild1.addChild(new Node(4));
let leaf2 = rootChild1.addChild(new Node(5));
let output = bfs(root);
console.log(output); // --> [1, 2, 3, 4, 5]

leaf1.addChild(new Node(6));
rootChild2.addChild(new Node(7));
output = bfs(root);
console.log(output); // --> [1, 2, 3, 4, 5, 7, 6]

 

 

이미 짜여진 코드:

let bfs = function (node) {
  // TODO: 여기에 코드를 작성합니다.
};

// 이 아래 코드는 변경하지 않아도 됩니다. 자유롭게 참고하세요.
let Node = function (value) {
  this.value = value;
  this.children = [];
};

// 위 Node 객체로 구성되는 트리는 매우 단순한 형태의 트리입니다.
// membership check(중복 확인)를 따로 하지 않습니다.
Node.prototype.addChild = function (child) {
  this.children.push(child);
  return child;
};

 

 

📝 이 문제는... 

bfs(너비 우선 탐색, Depth-First Search)와 dfs(깊이 우선 탐색,Breadth-First Search)의 차이를 알고 풀어야 하는 문제이다.

💡 잠깐! 아이디어 생각해보기

 

1. 노드 트리

 

트리 구조란 그래프의 일종으로, 한 노드에서 시작해서 다른 정점들을 순회하여 자기 자신에게 돌아오는 순환이 없는 연결 그래프이다.

 

위 그림에 대한 설명은 다음의 링크에서 자세히 볼 수 있다.

어쨌든 중요한점은 노드들이 이와 같이 트리구조로 이루어져있고,

트리의 높이란, 루트 노드에서 가장 깊숙히 있는 노드의 깊이를 의미한다는 점이다.

 

트리를 흔히 '그래프'라고도 부른다.

정리하자면, 그래프란, 정점(node)와 그 정점을 연결하는 간선(edge)로 이루어진 자료구조이다.

 

 

2. 그래프를 탐색하는 방법 두가지, 너비 우선 탐색 vs 깊이 우선 탐색

 

그래프를 탐색한다는 것은 하나의 정점부터 차례로 모든 정점을 방문하는 것을 말한다.

그리고 그 방법엔 두가지가 있다.

  • bfs(너비 우선 탐색, Depth-First Search)
  • dfs(깊이 우선 탐색,Breadth-First Search)

 

 

  너비우선탐색 깊이우선탐색
순서 1. 시작 정점 방문
2. 인접한 모든 정점 우선 방문
3. 더이상 방문할 정점이 없으면 한단계 아래로 내려감
4. 더이상 방문할 정점이 없을 때까지 2와 3의 반복		 1. 시작 정점 방문
2. 자식 모두 탐색
3. 또 자식이 있으면 그 아래 자식 탐색
4. 더이상 내려갈 정점이 없을 때까지 2와 3의 반복
5. 상위 정점으로 돌아와서 
6. 더이상 내려갈 정점이 없을 때까지 2와 3의 반복
구현법 큐 스택 또는 재귀함수
강점 - 최단 경로를 찾을 수 있다.
- 노드 수가 적고 깊이가 얕을 때 좋다
- 모든 경우를 하나하나 다 탐색해야하는 경우 좋다.		 - BFS에 비해 저장공간의 필요성이 적다.
- 찾아야 하는 노드가 깊은 단계에 있을 수록 좋다.
- 노드가 좌측에 있을 때 좋다.
- 그래프가 엄청 크면 DFS가 나을 수 있다.
- 구현하기 더 간단하다.
약점 - '큐'에 따로 탐색할 노드들을 저장해 두어야 해서 저장공간이 많이 필요하다.
- 노드의 수가 늘어나면 탐색해야하는 노드가 많아지기 때문에 비효율적이다.		 - 찾은 노드가 최단 경로라는 보장이 없다.
- 깊이 들어갔다가 헛수고 할 위험이 있다.
문제유형 - 경로의 특징을 저장해둬야 하는 문제 (a부터 b까지 가는데 같은 정점은 두번 지나면 안된다 같은) - 최단거리 구하는 문제 (미로찾기 같은)
실사용 - 미로 - 친구찾기 & 친밀도 계산
- p2p 네트워크에서 인접 노드 찾기
- 웹 크롤러

 

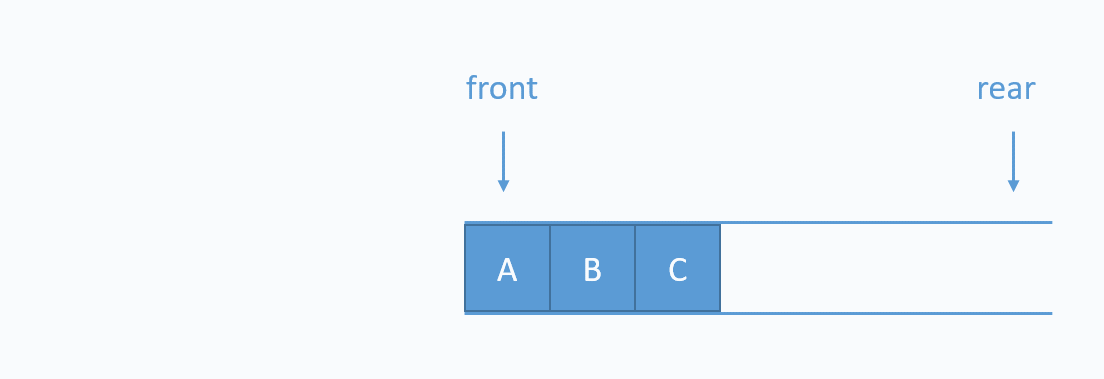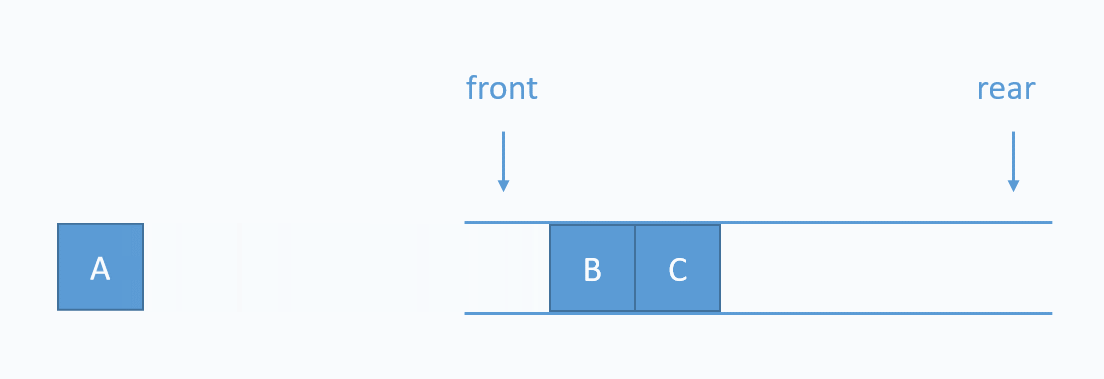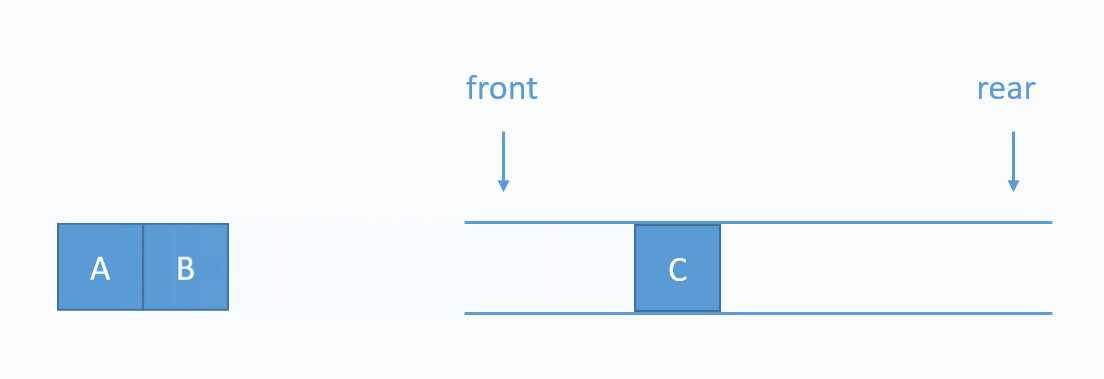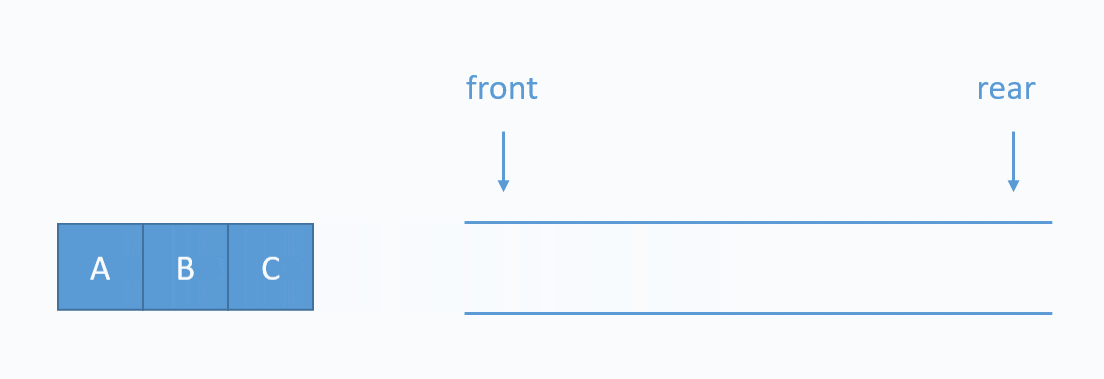
3. 큐

큐(Queue)는 영어로 '대기줄'을 의미한다. 

버스 대기줄을 생각해볼때, 먼저 줄 선 사람이 당연히 먼저 차에 탈 것이다.

큐는 이렇게 선입 선출(FIFO, First In First Out) 자료 구조를 의미한다.

 

 

 

이때 자료를 줄세우는 것을 Enqeue라고 한다.

아래의 gif를 참고한다.

 

이미지 출처: https://www.programmersought.com/article/59436057429/

 

또 자료가 하나씩 빠져나가는 것을 Deqeue라고 한다.

아래의 gif를 참고한다.

 

이미지 출처: https://www.programmersought.com/article/59436057429/

 

🌟 문제풀이

 

 

//------- ✏️ 작성 코드 여기부터 -------
let bfs = function (node) {
  const queue = [node] // 첫 노드 깔아놓고 시작
  const result = []

  while(queue.length > 0){
    const head = queue.pop() //queue *맨끝(가장 오른쪽)*요소를 하나 없애고 없앤 요소를 할당
    
    result.push(head.value) // 없앤 거는 result 맨 끝에 차례로 붙이기
    // qeue에서 늦게 사라졌을수록 오른쪽 끝에 붙음
    
    head.children.forEach((child) => {queue.unshift(child)}) 
    //자식들은 순서대로 queue *맨앞(가장 왼쪽)*에 붙이기
  }

  return result;
  
};
//------- ✏️ 작성 코드 끝-------



let Node = function (value) {
  this.value = value;
  this.children = [];
};

Node.prototype.addChild = function (child) {
  this.children.push(child);
  return child;
};

 

 

위의 코드는 배열의 왼쪽으로 들어가서 오른쪽으로 나오는 시나리오다.

아래의 이미지 처럼!

이미지 출처: https://lemidia.github.io/data%20structure/queue/

 

물론

qeue.pop() => que.shift(),

qeue.unshift() => qeue.push() 로 바꾸면 

 

오른쪽에서 들어와서 왼쪽으로 나가는 큐가 될것이다.

방향이 어느쪽이든 선입선출 잘해주고, result에 빠져나간 순서대로 push만 잘해주면 상관없다.